Identifying protein complexes in high-throughput data using Markov Random Fields

W. Rungsarityotin, R. Krause, A. Schliep, Max Planck Institute for Molecular Genetics.
A. Schödl, Think-cell Software.

Availability

The source code is available and can be downloaded as a gzip-tar archive from here.

Background

Predicting protein complexes from the high-throughput experimental data remains a challenge due to uncertainty in their observation. Current methods typically rely on heuristics to first construct an interaction graph from the data and subsequently apply a graph-based clustering method to identify protein complexes. In contrast, we propose a model-based prediction of protein complexes which uses the observations directly.

Result

We model purifications as observations of protein complexes and formulate a model of protein complexes based on Markov Random Fields incorporating the false negative and false positive rate. We apply our model to predict complexes from the data obtained from hight-throughput experiments without prior elimination of proteins from the sets. We provide an elegant solution to the problem that compares well to other prediction made by two clustering algorithms and to reference data set, particularly for larger unfiltered data sets.

Supplementary materials

Clusters from MRF

We order the clusters from the highest quality to lowest quality according to the quality score. For each cluster, an assignment to an annotated complex (both MIPS or Reguly) is decided by majority voting with at least half of the proteins in the cluster belonging to that complex.

Spoke model:

Matrix model:

Matching to MIPS complexes

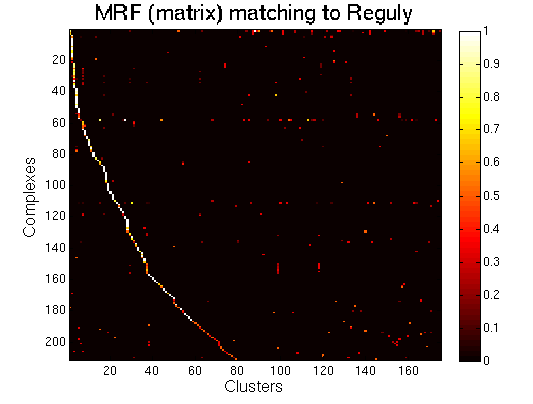
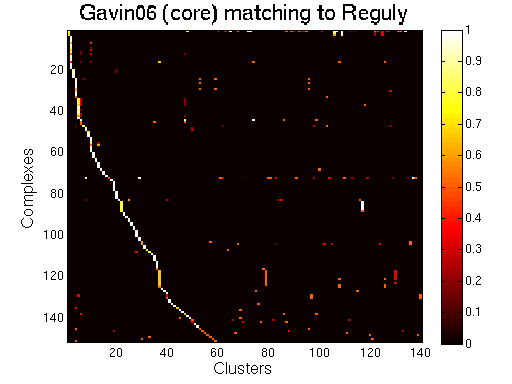
For each clustering solution, we can visualize a matching to MIPS complexes by generating a contingency table whose rows are complexes and columns are clusters. For each cell (i,j) in the table, we count the number of proteins in common between the ith complex and the jth cluster and calculate the Simpson coefficient. We order the diagonal of the table by increasing matching sizes. Clusters without a match to an annotated complex are not part of the table, likewise for complexes without matching to a cluster. The number of clusters and complexes are different for each table. The order of complexes are not the same in all plots.

Data set: Gavin06.
Color scale: Bright color indicates higher Simpson coefficient. See colorbar.

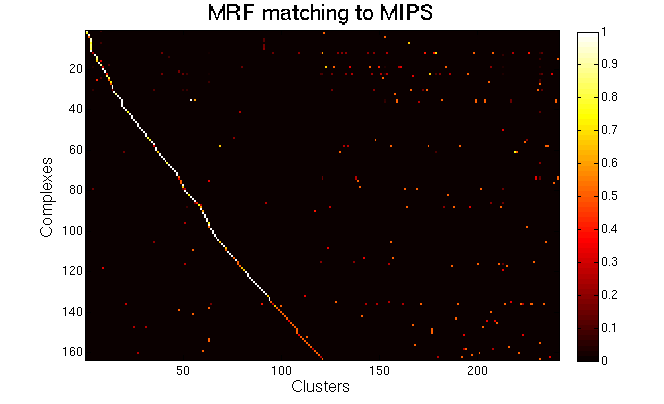
	MRF (spoke model). high resolution diagonal matches
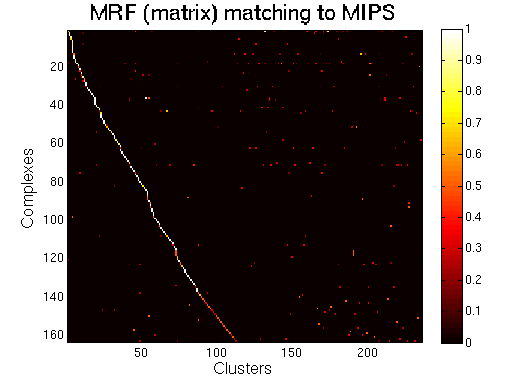
	MRF (matrix model). high resolution diagonal matches
	A solution from MCL with the first cluster as a giant component merging several complexes. high resolution diagonal matches
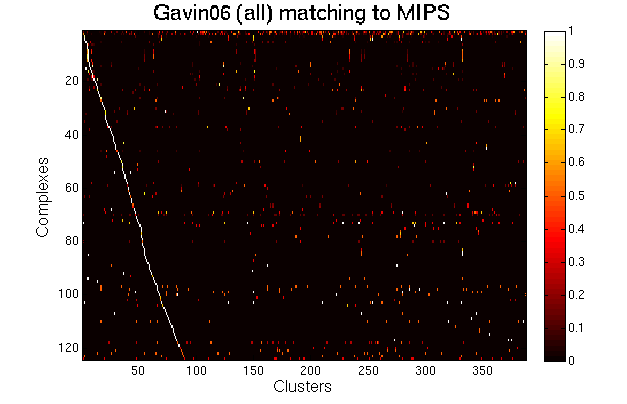
	Gavin06 solution including cores, modules and attachments. This solution has many overlapping clusters due to modules and attachments. high resolution diagonal matches
	The core components of the Gavin06 solution. high resolution diagonal matches

Matching to Reguly

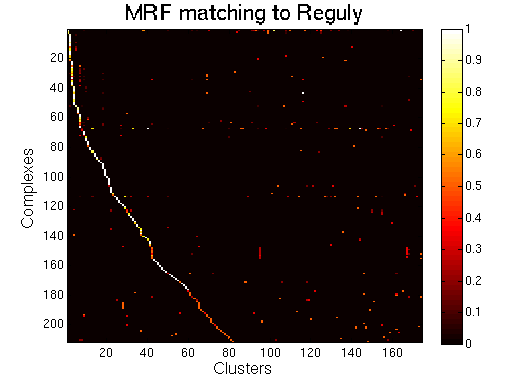
	MRF (spoke model). high resolution
	MRF (matrix model). high resolution
	MCL. high resolution
	Gavin06 (core). high resolution

Contact: Alexander Schliep